Semiramis

Os artistas da Renascença designaram por número de ouro, um número que, desde a mais remota antiguidade, era visto como símbolo cosmológico e fórmula mágica. Pelas propriedades de que goza , o número de ouro é chave de diversas construções geométricas utilizadas, desde há muitos séculos, na Arquitectura; a proporção que ele traduz é considerada particularmente estética e numerosas obras primas da pintura e da escultura inspiraram-se nele. O número de ouro também chamado Divina Proporção desde que Fra Luca Paccioli, sob a influência de Piero de La Francesca, escreveu um livro sobre este número com desenhos de Leonardo da Vinci (o primeiro a utilizar a expressão sectia aurea), é talvez, de todos os números, o mais famoso e ubíquo. No século XX o arquitecto Le Corbusier (1948) fundamentou nas propriedades do número de ouro, o seu MODULOR, espécie de tabela, com medidas padrão, a ser utilizada nas obras arquitectónicas.

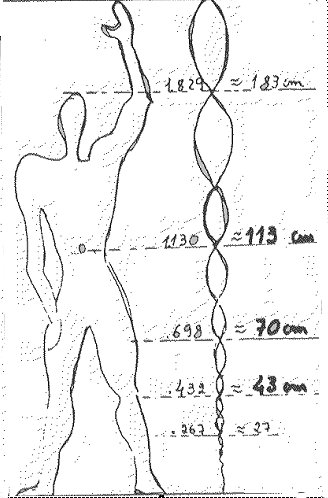
O MODULOR. módulo de ouro, é uma tabela para uso da Arquitectura, inspirada no número de ouro Φ. Le Corbusier construiu-a tomando como base três medidas aproximadas, 43cm, 70cm e 113cm, onde 113 = 70 + 43 e cuja razão é o número de ouro. Note-se que a secção áurea de 113 é 70; que a de 70 é 43 = 113 - 70; que a de 43 será 27 = 70 - 43, e assim sucessivamente. Assim, Le Corbusier parte de 113 e continua, nos dois sentidos, construindo uma cadeia de secções áureas a que chamou série vermelha:

4 - 6 - 10 - 16 - 27 - 43 - 70 - 113 - 183 - 296

A estatura humana correspondia à medida de referência 183cm. A altura ao solo do umbigo seria de 113 cm; o joelho situar-se-ia a 43cm, etc.. As medidas da série vermelha foram, por Le Corbusier, tomadas como base para o estudo das alturas das bermas, bancadas, cadeiras, mesas, balcões, janelas, muros, portas, tectos, etc..

Matematicamente, número de ouro é a raiz positiva da equação: x2 – x – 1 = 0. É uma dízima infinita não periódica. Com dez casas decimais podemos escrever Φ = 1,6180339887.... Também pode ser obtido através da sucessão de Fibonacci, cuja principal propriedade é que cada termo é a soma dos dois termos que o antecedem.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 ...

A razão entre cada termo desta sucessão e o anterior converge rapidamente para o número Phi, que é o limite dessa sucessão. O seu inverso representa 0, 618033 também um papel importante na proporção áurea. O inverso do número de ouro é a raiz positiva da equação: x2 + x – 1 = 0.
No caso de Le Corbusier, este aplicou aquela proporção partindo de um valor de referência (183 cm). Construiu portanto uma sucessão com valores diferentes da de Fibonacci, mas com a mesma razão entre os números consecutivos.

Geometricamente o número de ouro pode ainda ser calculado pela razão entre a diagonal e o lado de um pentágono regular. Ou seja, pela razão entre uma qualquer das linhas do pentagrama e a distância entre duas extremidades contíguas do mesmo. Sendo assim, o número de ouro pode ser obtido pela expressão 0,5*(1 + RQ(5)), onde RQ significa raiz quadrada. Obviamente estas coincidências excitam as imaginações e facilitam a elaboração de especulações esotéricas.

O número de ouro é muitas vezes relacionado com o chamado "rectângulo de ouro", que tem intrigado estudiosos desde há muitos anos atrás. Este rectângulo baseia-se no seguinte princípio formulado pelo alemão Zeizing, em 1855:

Para que um todo dividido em duas partes desiguais pareça belo do ponto de vista da forma, deve apresentar a parte menor e a maior a mesma relação que entre esta e o todo.

Ou seja, dado um segmento de recta AB, um ponto C divide este segmento de uma forma mais harmoniosa se existir a proporção de ouro AB/CB = CB/AC (sendo CB o segmento maior). O número de ouro é exactamente o valor da razão AB/CB, a chamada razão de ouro. O rectângulo de ouro goza da seguinte propriedade: suprimindo-lhe o quadrado de lado igual ao seu lado menor, sobra um rectângulo com as mesmas proporções que o primeiro, isto é, semelhante ao primeiro. Se a cada rectângulo áureo se retirar o quadrado de lado menor obtém-se outro rectângulo áureo, e assim sucessivamente

Portanto, se desenharmos um rectângulo cuja razão, entre os comprimentos dos lados maior e menor, é igual ao número de ouro, obtemos um rectângulo de ouro. O rectângulo de ouro é uma entidade matemática que marca forte presença no domínio das artes, nomeadamente na arquitectura, na pintura, e até na publicidade. Este facto não é uma simples coincidência já que muitos testes psicológicos demonstraram que o rectângulo de ouro é de todos os rectângulos o mais agradável à vista. Por exemplo, o Parténon, em Atenas, está calculado com base no número de ouro, visto que a Arquitectura grega considerava a proporção áurea como a proporção perfeita, o máximo da harmonia. Inclusive na Grande Pirâmide de Gizé, construída pelos egípcios, o quociente entre a altura de uma face pela metade do lado da base é quase 1,618, embora há 45 séculos ninguém tivesse alguma vez ouvido falar no número Phi.

A divisão de um segmento de recta feita segundo essa proporção, denomina-se divisão áurea, a que Euclides chamou divisão em média e extrema razão, também conhecida por secção divina ou secção áurea, segundo Leonardo da Vinci, como escrevi acima. No fundo a formulação é simples: Para seccionar um todo em partes desiguais, de modo a obter equilíbrio e beleza, é preciso que a razão entre o todo e a parte maior seja igual à razão entre esta e a parte menor. Portanto o número de ouro aplica-se ao rectângulo, mas igualmente à divisão em troços de um segmento de recta.

Até hoje não se conseguiu descobrir a razão de ser dessa beleza, mas a verdade é que existem inúmeros exemplos onde o rectângulo de ouro aparece. Até mesmo nas situações mais práticas do nosso quotidiano, encontramos aproximações do rectângulo de ouro, é por exemplo o caso dos cartões de crédito e outros documentos do género, assim como a forma rectangular de muitos dos nossos livros, embora ultimamente, por questões de normalização na dobragem do papel, a relação entre os lados das folhas de papel normalizado esteja na proporção da raiz quadrada: A0, A1, ...,A4, A5, etc...

Todavia não é verdade que as proporções dos seres humanos «se ajustem com flagrante exactidão a esse rácio», como escreve o autor do Código da Vinci. As pessoas não são todas iguais, nem têm todas as mesmas proporções. O que é todavia verdade é que essas proporções são vistas como um ideal de beleza. Isto é, segundo os nossos critérios de estética sobre as proporções das coisas e das pessoas, quando essas proporções estão de acordo com o número de ouro, consideramo-las mais belas.

Talvez por isso, os egípcios do tempo de Khéops tenham utilizado um valor aproximado àquela proporção na Grande Pirâmide, embora nada permita concluir tenham sido guiados pelo número Phi.

Nota: Ver O Número de Ouro in Boletim da Sociedade Portuguesa de Matemática nº 17 (Junho 1990), nº 19 (Fevereiro 1991) e nº 20 (Junho 1991)

Nota - Ler ainda 1, 3, 4 e 5